Sumber gambar : Dokumen Penulis
Selamat datang di blog Saya Anak Cerdas! Apa kabar, Sahabat Cerdas? Semoga hari Anda selalu menyenangkan. Pada postingan ini, saya akan membahas kembali materi MATEMATIKA yakni ilmu yang menyenangkan, hihihi. Kali ini saya akan mengulas tentang dua jenis bangun ruang yaitu BALOK dan KUBUS. Selamat belajar!
BALOK
#1. Pengertian Balok
Sumber gambar : Dokumen Penulis
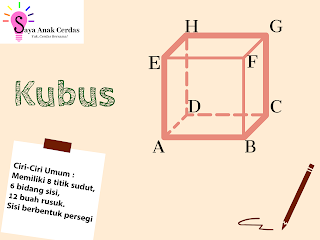
Kubus
Kubus adalah salah satu jenis bangun ruang atau tiga dimensi yang dibentuk oleh 6 buah bidang sisi segi empat sama panjang (pesergi). Kubus bisa dikatakan sebagai saudara dari balok karena memiliki beberapa kesamaan.
#2. Ciri-Ciri Kubus
Kubus memiliki ciri-ciri atau sifat-sifat sebagai berikut.
- Memiliki 6 bidang sisi yang berbentuk segi empat beraturan atau persegi.
- Memiliki 8 titik sudut
- Mempunyai 12 buah rusuk.
- Terdapat 4 digonal ruang
- Semua sisinya sama luas.
- Memiliki 12 diagonal bidang yang sama panjang
#3. Rumus Balok dan Contoh Soal
1. Volume
Cara menghitung volume kubus menggunakan rumus sisi x sisi x sisi atau sisi pangkat 3
Rumus :
Volume Kubus = S x S x S
2. Luas Permukaan
Berikut rumus mencari luas permukaan.
Rumus :
Luas Permukaan = 6 x S x S
= 6 x S²
Rumus di atas didapat karena jumlah sisi pada kubus berjumlah 6 bidang dan rumus luas persegi pada kubus adalah S x S atau S².
3. Diagonal Bidang
Cara menghitung panjang diagonal bidang pada kubus adalah
Rumus :
Diagonal Bidang = s√2
4. Diagonal Ruang
Rumus mencari panjang diagonal ruang pada kubus adalah
Rumus :
Diagonal Ruang = s√3
Contoh Soal :
Sania memiliki sebuah kotak mainan diberi nama ABCD.EFGH berbentuk kubus dengan ukuran 15 cm x 15 cm. Hitunglah pada kotak tersebut :
a. Volume
b. Luas Permukaan
c. Diagonal Bidang AE
d. Diagonal Ruang AG
Penyelesaian :
Sumber gambar : Dokumen Penulis
BALOK
#1. Pengertian Balok
Sumber gambar : Dokumen Penulis
Balok
Balok adalah salah satu bangun ruang segi empat yang terdiri dari 6 buah bidang sisi atau 3 pasang sisi ( 2 pasang sisi berbentuk persegi panjang dan paling tidak 1 pasang sisinya lagi bebentuk segi empat berbeda ukuran).
#2. Ciri-Ciri Balok
Ciri-ciri atau sifat-sifat dari balok yaitu sebagai berikut.
- Memiliki 3 Pasang bidang sisi atau 6 buah sisi (2 pasang sisi berbentuk persegi panjang dan 1 pasang sisi berbentuk segi empat dengan ukuran berbeda.
- Memiliki 12 buah rusuk.
- Mempunyai 8 titik sudut
- Terdapat 3 elemen, yakni panjang (p), lebar (l), dan tinggi (t)
- Rusuk- rusuk yang sejajar sama panjang.
- Diagonal ruang pada balok memiliki panjang yang sama.
#3. Rumus Kubus dan Contoh Soal
1. Volume
Balok memiliki rumus yang berbeda dengan kubus karena ukuran yang berbeda. Balok memiliki tiga elemen utama yakni panjang (p), lebar (l), dan tinggi (t). Maka dari itu cara menghitung volume balok adalah
Rumus :
Volume Balok = p x l x t
2. Luas Permukaan
Cara menghitung luas permukaan pada balok adalah sebagai berikut.
Rumus :
Luas Permukaan = 2(p.l + p.t + l.t)
3. Diagonal Ruang
Berikut rumus yang digunakan untuk mencari panjang diagonal ruang pada balok.
Rumus :
Diagonal Ruang = √p² + l² + t²
4. Diagonal Bidang
Untuk mengetahui seberapa panjang diagonal bidang pada balok dapat dihitung dengan rumus PYTHAGORAS (yang digunakan adalah rumus mencari garis miring). Rumus diagonal bidang balok ada 3, tergantung di sisi mana diagonal bidang yang dicari itu terletak
Rumus :
Diagonal Bidang
= √p²+t² (sisi depan & belakang)
= √p² + l² (sisi atas & bawah)
= √l² + t² (sisi samping kanan & kiri)
Contoh Soal :
Sebuah balok yang diberi nama balok ABCD.EFGH dengan ukuran panjang 8 cm, lebar 4 cm, dan tinggi 6 cm. Tentukanlah :
a. Volume
b. Luas Permukaan
c. Diagonal Ruang garis AG
d. Diagonal Bidang garis BE
Penyelesaian :
Diketahui :
Panjang = 8 cm
Lebar = 4 cm
Tinggi = 6 cm
a. Volume = p x l x t
= 8 x 4 x 6
= 72 cm pangkat 3
b. Luas Permukaan = 2(p.l + p.t + l.t)
= 2((8 x 4) + (8 x 6) + (4 x 6))
= 2 (32+48+24)
= 2 (104)
= 208 cm²
c. Diagonal Ruang AG = √p² + l² + t²
= √8² + 4² + 6²
= √64 + 16 +36
= √116 cm
d. Diagonal Bidang AE =
Sumber gambar : Dokumen Penulis
Rangkuman Rumus :
Sumber gambar : Dokumen Penulis
Jadi bagaimana? Sudah paham mengenai kubus dan balok. Sekedar tips, dalam belajar matematika memahami konsep materi lebih penting daripada menghafal. sekian dulu materi kali ini. Tetap semangat, sampai jumpa.





Komentar
Posting Komentar
Terima kasih sudah berkunjung ke blog Saya Anak Cerdas. Silakan berkomentar sesuai dengan pembahasan, bijak, dan tidak memuat link aktif.